本题的推导过程非常复杂,但最终的程序运行很快。以下仅给出主要步骤,这些步骤系摘自官方论坛。
首先应当观察到给定不共线的四点,若其组成凸四边形,那么所对应的凸四边形只有一个,但若其组成凹四边形,则有三种组法,如下图:
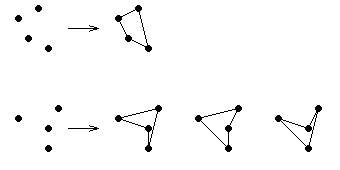
要找到不共线的四点,可以先找出不共线的三点,然后分别统计其内部和外部的点,内部的点与这三点共同形成凹四边形,外部与三条边都不共线的点与之组成凸四边形。
三角形边界及其所在直线上的点的数量可以直接计算,内部的点的数量可以用Pick定理计算,从点的总数中去除这两者就是外部不共线的点的数量,最后用容纳原理排除重复。
经过复杂的计算,可得
$$Q(m,n)=\binom{(m+1)(n+1)}{4}-\binom{(m+1)(n+1)}{3}+2S+\left(7-2(m+1)(n+1)\right)L_3+7L_4$$
其中$S$是此范围内所有三角形面积之和,$L_3$和$L_4$分别是三线共点和四线共点的情况总数且有具体公式
\begin{align*}
S&=\sum_{x=0}^m\sum_{y=0}^n\frac{11x^2y^2+x^2+y^2-\gcd^2(x,y)}{6}(m-x+1)(n-y+1) \\
L_3&=\sum_{x=1}^m\sum_{y=1}^n2(\gcd(x,y)-1)(m-x+1)(n-y+1)+\sum_{x=1}^m(x-1)(m-x+1)(n+1)+\sum_{y=1}^n(y-1)(n-y+1)(m+1) \\
L_4&=\sum_{x=1}^m\sum_{y=1}^n(\gcd(x,y)-1)(\gcd(x,y)-2)(m-x+1)(n-y+1)+\sum_{x=1}^m\frac{(x-1)(x-2)}{2}(m-x+1)(n+1)+\sum_{y=1}^n\frac{(y-1)}{2}(n-y+1)(m+1)
\end{align*}
用$G(a,b)$表示范围内互素的$x^ay^b$之和,用$H(a,b,c)$表示范围内$x^ay^b\gcd(x,y)^c$之和,将上述各项利用求和公式用G和H表示,其中G可以用记忆化搜索递归计算,最终结果是$104354107$。
注:因使用cache装饰器作记忆化搜索,以下代码为Python 3。
import math
from functools import *
m,n=12345,6789
mod=135707531
S=lambda t,k:[t,t*(t+1)//2,t*(t+1)*(2*t+1)//6,t*t*(t+1)*(t+1)//4,t*(t+1)*(2*t+1)*(3*t*t+3*t-1)//30][k]
@cache
def G(u,v,a,b):
q=math.isqrt(u)
res=S(u,a)*S(v,b)-sum(G(u//k,v//k,a,b)*(k**(a+b)) for k in range(2,min(v,u//q)+1))
for k in range(1,q):
x=v//(u//(k+1)+1)
y=v//(u//k)
if x==y:
res-=G(k,x,a,b)*(S(u//k,a+b)-S(u//(k+1),a+b))
else:
res-=G(k,x,a,b)*(S(min(u//k,v//x),a+b)-S(max(u//(k+1),v//(x+1)),a+b))
if y:
res-=G(k,y,a,b)*(S(min(u//k,v//y),a+b)-S(max(u//(k+1),v//(y+1)),a+b))
return res
def H(a,b,c):
if c==0:
return S(m,a)*S(n,b)
q=math.isqrt(m)
res=sum(G(m//k,n//k,a,b)*(k**(a+b+c)) for k in range(1,min(n,m//q)+1))
for k in range(1,q):
x=n//(m//(k+1)+1)
y=n//(m//k)
if x==y:
res+=G(k,x,a,b)*(S(m//k,a+b+c)-S(m//(k+1),a+b+c))
else:
res+=G(k,x,a,b)*(S(min(m//k,n//x),a+b+c)-S(max(m//(k+1),n//(x+1)),a+b+c))
if y:
res+=G(k,y,a,b)*(S(min(m//k,n//y),a+b+c)-S(max(m//(k+1),n//(y+1)),a+b+c))
return res
f=lambda a,b,c:H(a,b,c)+(a==0)*S(n,b+c)+(b==0)*(S(m,a+c))+(a+b+c==0)
s001=f(0,0,1)
s011=f(0,1,1)
s101=f(1,0,1)
s111=f(1,1,1)
s002=f(0,0,2)
s012=f(0,1,2)
s102=f(1,0,2)
s112=f(1,1,2)
s000=f(0,0,0)
s010=f(0,1,0)
s100=f(1,0,0)
s110=f(1,1,0)
s330=f(3,3,0)
s320=f(3,2,0)
s230=f(2,3,0)
s220=f(2,2,0)
s310=f(3,1,0)
s210=f(2,1,0)
s300=f(3,0,0)
s200=f(2,0,0)
s130=f(1,3,0)
s120=f(1,2,0)
s030=f(0,3,0)
s020=f(0,2,0)
s=(s012-s230*11-s210-s030)*(m+1)+(s102-s320*11-s300-s120)*(n+1)-(s112-s330*11-s310-s130)-(s002-s220*11-s200-s020)*(m+1)*(n+1)
c3=2*((s010-s011)*(m+1)+(s100-s101)*(n+1)-(s000-s001)*(m+1)*(n+1)-(s110-s111))+s020-(n+2)*s010+(n+1)*s000+s200-(m+2)*s100+(m+1)*s000
c4=(s000*4-s001*6+s002*2)*(m+1)*(n+1)+(s110*4-s111*6+s112*2)-(s100*4-s101*6+s102*2)*(n+1)-(s010*4-s011*6+s012*2)*(m+1)+s030-(n+4)*s020+(3*n+5)*s010-2*(n+1)*s000+s300-(m+4)*s200+(3*m+5)*s100-2*(m+1)*s000
print((math.comb((m+1)*(n+1),4)-math.comb((m+1)*(n+1),3)+s//3+(7-2*(m+1)*(n+1))*c3+7*c4//2)%mod)
|