$N$个座位排成一排，$N$个人根据以下规则依次坐到座位上：

第一个人可以选择任意位置坐下，之后每人都选择与已经坐下的人相隔尽可能远的座位，若可能的选择有多个，则选择其中最左边的座位，此外任意两人都不能相邻（也就是任意两人之间至少有一个空座位）。

显然不能相邻的规则使得有些座位一定会空着，因此能坐下的人的总数数一定比N小。下图展示了$N=15$时所有可能的坐法：

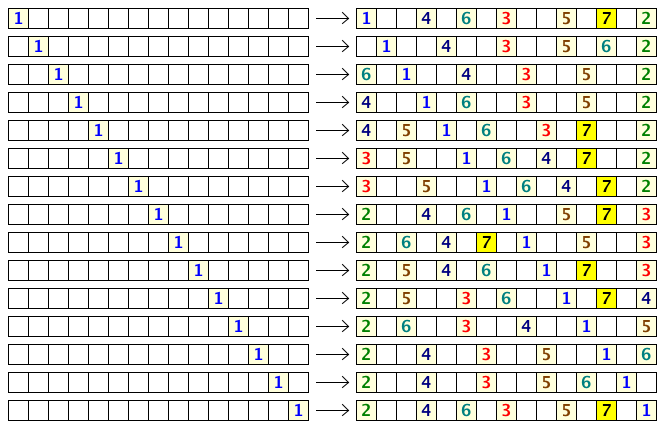
可以看出若第一个人选择了合适的位置时$15$个座位最多可以坐下$7$人，且能达到此最大值的第一个人的坐法共有$9$种。

记$f(N)$是使得$N$个座位能坐下最多的人的第一个人的坐法总数，可以验证$f(1)=1, f(15)=9, f(20)=6, f(500)=16$，此外还有$\sum_{N=1}^{20}f(N)=83$以及$\sum_{N=1}^{500}f(N)=13343$。

求$\sum_{N=1}^{10^{12}}f(N)$的最后八位数字。

本题难度:

解答

本题的探索过程十分繁琐，以下解答整合自官方论坛。

首先注意到坐下的人数最多时两端不能都是空位，否则只需每人左移一格就可以在右侧末尾再增加一人。

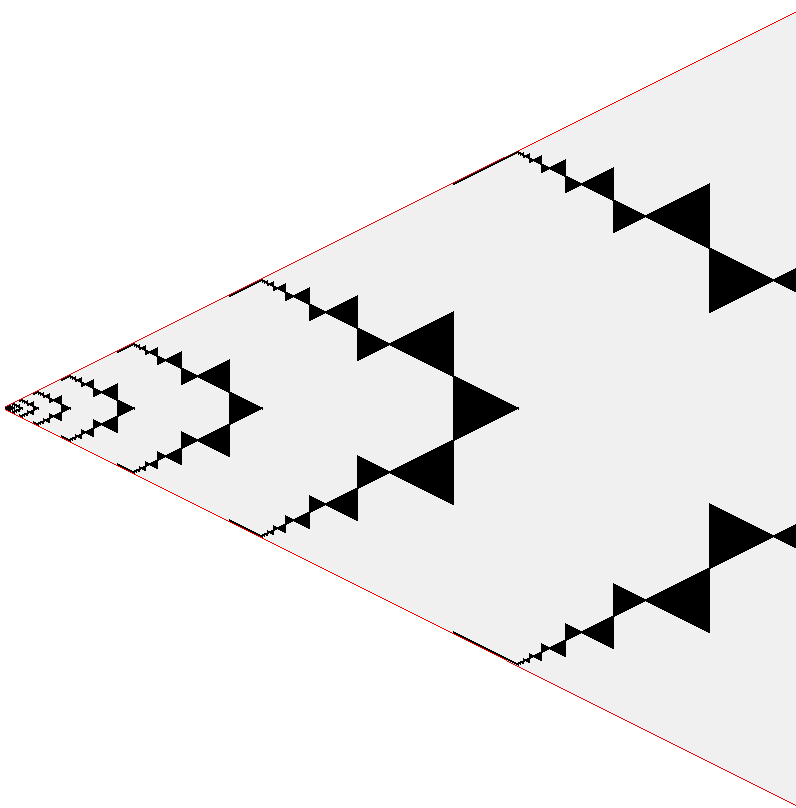
令$g(N)$为有$N$个座位且第一个人坐在最左侧或最右侧时（显然由对称性可知两者相同）能够坐下的最多人数，则当第一个人坐在第$k$个位置时能坐下的最多人数是$g(k)+g(N-k+1)-1$，其中$g(k)$表示前$k$个位置能容纳的最多人数（第$k$个位置处其是最后一人），$g(N-k+1)$表示第$k$个位置到第$N$个位置能容纳的最多人数（第$k$个位置处其是其第一人），此过程中第$k$个位置计入了两次，因此最后减去$1$。从而 $$g(N)=\max_k g(k)+g(N-k+1)-1, \quad f(N)=|\{k: g(k)+g(N-k+1)-1=g(N)\}|.$$ 由此可得 $$g(N)=\max(N-2^m, 2^{m-1}+1), \quad m=\lfloor\log_2(N-1)\rfloor.$$ 从而$f(N)$具有分段常数和自重复的分形特征，若分别以$x=k$和$y=N-k+1$为轴，则取到$g(N)$的点如下（图片来自官网论坛）

令$S(N)=\sum_{i=1}^Nf(i)$，则 $$S(2^n+1)=4S(2^{n-1}+1)-25\cdot2^{n-3}-13(n-4)+1.$$ 由于$2^{39} < 10^{12} < 2^{40}$，可以先取$n=40$得$S(2^{40}+1) \bmod 10^8=S(1099511627777) \bmod 10^8=51861893$。

而上式中多计算的$99511627777$项$f(i)$的值似乎恰好从$3$取至$99511627779$，因此最终结果是 $$51861893-\frac{99511627777\cdot(3+99511627779)}{2} \bmod 10^8=73811586.$$ 本题无需编程。